[9]Approximation Algorithm
Exact Algorithm指的是可以找到最佳解的,像前面講過的多數演算法,且這些演算法從行為上都稱為Deterministic Algorithm,代表有固定的步驟可以去完成。我們沒有辦法幫NPC問題找到Exact Algorithm得到最佳解,因此,我們改成追求Approximation Algorithm。
一個可行的辦法是用Heuristic algorithm,現實上多是用這樣的方法,算是一個堪用的方法。
Approximation Ratio
評估你找到的答案和最佳解差多少。用Opt(x)表示最佳解的值;A(x)是我們找到的Approximation Algorithm。令A為一ε-Approximation algorithm,那麼A會滿足
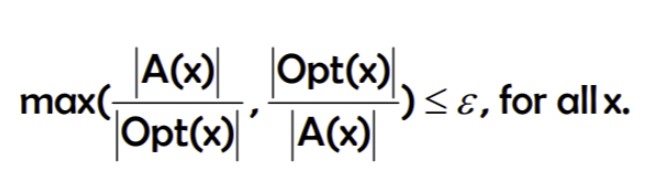
其中,ε就稱為Approximation Ratio;max可以指minimization和minimization。
但其中最神秘的就是 我們就是無法求出最佳解,要怎麼算ratio呢?
Vertex Cover
Vertex Cover是一NP-Hard問題(他的decision version是NP-Complete),下面舉的例子是Approximation Ratio < 2,稱為2-Approximation algorithm。(此類問題也有其他方法或許可以限定在更小的ε)
ApproxVC(G)
//input:G=(V,E)
//output:C for VC
C = ∅
E′ = E
While E′ ≠ ∅
Let(u,v) be an edge in E′
C = C ∪ (u,v)
remove every edge incident on u and v
Return C
Time complexity = O(|E|)。
圖示化
挑選移除圖中的一邊(B,C)[blue]並移除與知相鄰的邊(A,C)(C,D)(C,E)[yellow],重複動作直到所有的邊都被移除。
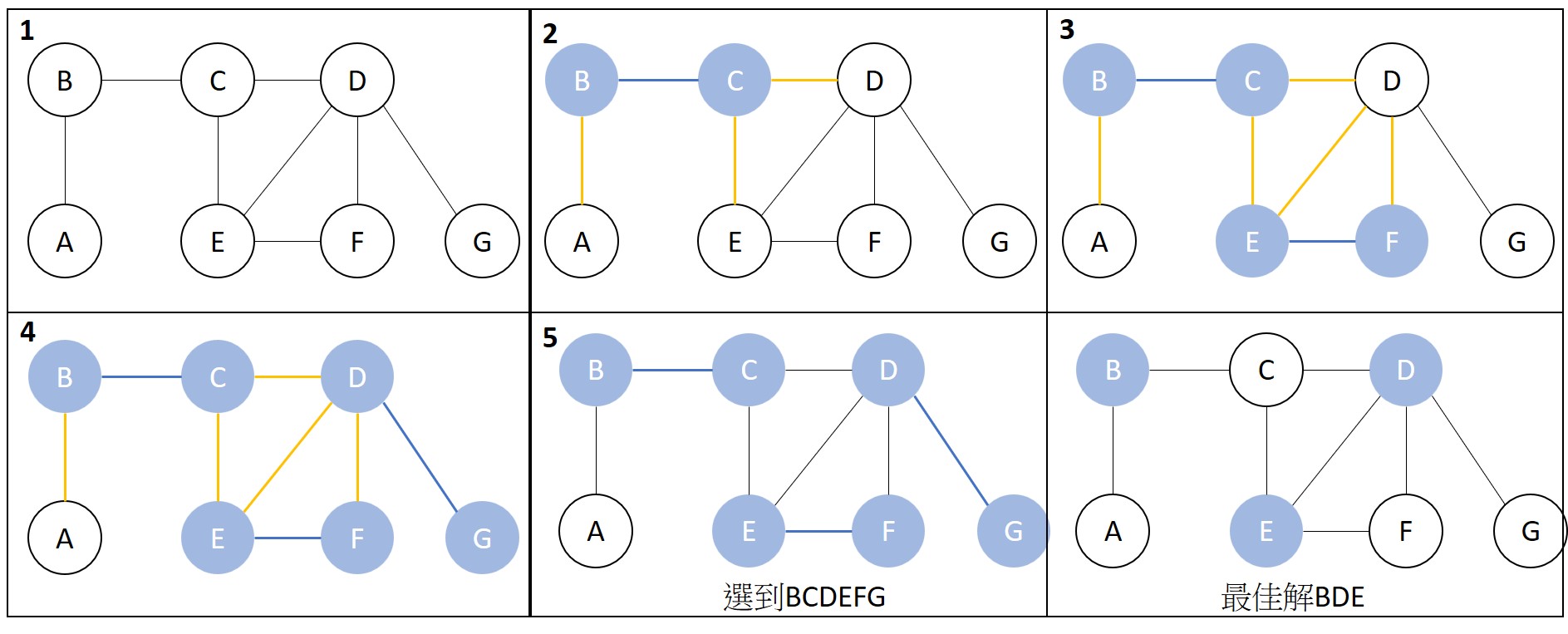
分析
- 假設剛才挑出的所有邊(上面藍色的)被放在集合A。
- 我們知道最佳解C*至少會cover A中每一邊的其中一點(否則C*就不會cover A,也就不是VC),所以可知|C*| ≧ |A|。
- 接著我們把在A當中的邊的兩端點都加入C,可知|C| = 2|A|。
最後可得|C| ≤ 2|C*|。
Euclidean TSP (ETSP)
證明ETSP可能出現在期末考!把TSP改成ETSP。
TSP是給予weighted complete graph,也就是權重可以隨意編寫;而ETSP是指點會在一二維平面上,所以兩點間的距離必須符合三角不等式。
ETSP(G)
//input: G = (V,E) and a start vertex c
//output: Hamiltonian Cycle
Select a vertex from V to be root
Compute MST T for G by using Prim
Let L be the list of vertices visited in a preorderd tree walk of T
Return Hamiltonian Cycle H that visits the verticed in the order L
圖示化
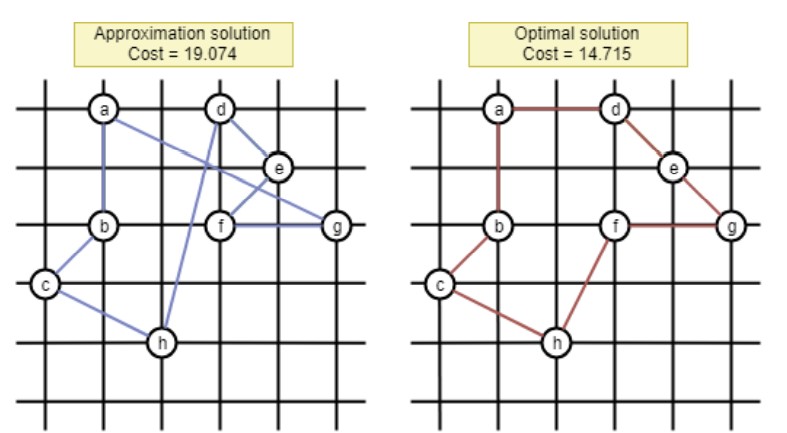
分析
令H*是最佳解。
cost(T) ≤ cost(H*),因為H*是一cycle,所以隨便刪掉一條邊來獲得一tree,tree的cost肯定會較小。
令W是一陣列儲存vertices的preorder full walk,full walk指的是恰好每條邊走兩次。
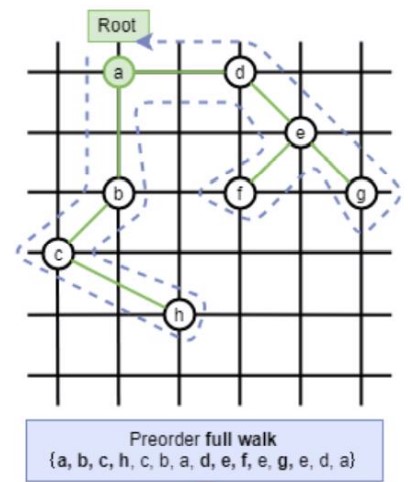
可知cost(W) = 2cost(T),可得 cost(W) ≤ 2cost(H*)。
令H是演算法找到的Hamiltonian Cycle。
可知cost(H) ≤ cost(W)。因為W是會走回上一點再往下一點去(父節點→左子節點→父節點→右子節點);H是加上三角不等式的概念,所以可以不用往回走(父節點→左子節點→右子節點)
最終可得cost(H) ≤ 2cost(H*)。
Polynomial-Time Approximation Scheme(PTAS)
- PTAS
上面是以倍數跟最佳解作比較,而這裡對倍數有更進一步的限制,定為1+ε(for minimization problem)、1-ε(for maximization problem)。例如ETSP問題,只要可以保證一演算法產生的解是(1+ε)L,其中L是最佳解,那麼就可以宣稱該演算法為PTAS。聽起來比上面用的不指定倍數值厲害許多,但是若時間複雜度為O(n^(1/ε)!)),那當ε很小,這樣的時間複雜度也是無法被接受的。
- EPTAS
多一個限制是O(n^c),且C和ε是獨立的。但依舊有點問題,例如是O(n+(1/ε)!)。
- FPTAS
演算法在n和1/ε都必須要是polynomial time。